实验结果分析

本文中闭孔泡沫铝材料采用熔体发泡法制备，平均胞元孔径~3 mm,相对密度p≈20%,密度变异系数(定义为标准差与密度平均值的比值)为8%。实验在MTS810材料试验机，分别在25℃(室温，RT),200℃,350℃和500℃条件下进行，实验温度偏差≤5℃。以位移控制方式加载，加载速率为0.06 mm/s。为得到温度对平台应力的影响，同时进行了各种相应温度下的单轴压缩实验。为保证实验的可重复性和有效性，实验中每种工况重复3次试验。具体实验细节如2.4节。

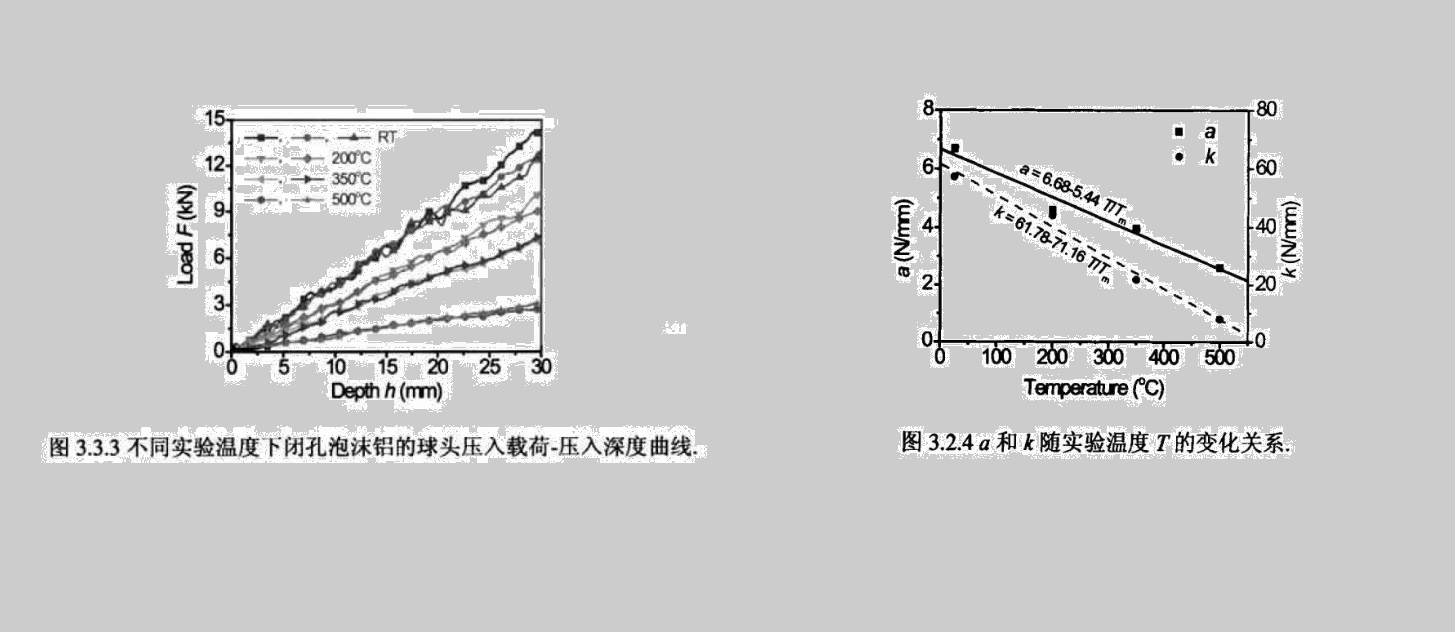
图3.3.3分别为闭孔泡沫铝在不同温度条件下半球形压头(Spherical-EndedPunch,SEP)压入时的载荷-深度响应曲线。闭孔泡沫铝在不同温度下的单轴压缩载荷-位移曲线具有典型的弹性段和表征胞壁塑性垮塌开始的峰值载荷，随后压垮载荷保持恒值或有轻微的应变硬化。随着实验温度的升高，泡沫铝单轴压缩的平台应力明显下降。SEP压入响应则不同，既没有明显的峰值载荷也没有明显的弹性段，压入载荷随着压入深度增大而持续增长。这是因为随着压入深度的增大，压头与泡沫铝的接触面积也在逐渐增大，因此相应的载荷也增大。但是随着实验温度的升高，泡沫铝的SEP压入载荷随压入深度增长的幅度越来越小。

由泡沫铝在不同温度下的单轴压缩实验可得泡沫铝在不同温度时的平台应力和压实应变。实验结果发现，闭孔泡沫铝平台应力o随温度升高线性降低，且可以用下式来表示

σpl=σ0pl·（1-T/Tm）                   (3.14)

式中，Tm是闭孔泡沫铝基体材料的熔化温度，本文中Tm=660℃。，σ0pl为参考温度T=0℃时闭孔泡沫铝的平台应力，通过数据拟合可得σ0pl=3.38 MPa,如图3.2.4所示。此外，闭孔泡沫铝的平台应力σpl和相对密度ρ有如下关系[6]

σpl=Cσysρn                             (3.15)

式中，参数C=0.25～0.35,n=1.5～2.0,σys为闭孔泡沫铝基体材料的屈服强度。基于Johnson-Cook模型，部分铝合金材料，如2024-T351等的屈服强度随温度的变化也是线性的,则有

σys=σ0ys（1-T/Tm）                         (3.16)

式中，σ0ys为参考温度T=0℃时闭孔泡沫铝基体材料的屈服强度。结合公式(3.14),(3.15)和(3.16)可得闭孔泡沫铝平台应力与相对密度和环境温度的关系

σ0pl/σ0ys=Cρn （1-T/Tm）                   (3.17)

根据上文压实应变的定义，不同温度下(-100℃～500℃)的实验结果发现压实应变对环境温度的变化并不敏感，如图2.2.5所示，其中低温数据来源于文献。故压实应变εd与环境温度T无关，只是相对密度ρ的函数。但是文献中对泡沫金属的压实应变与相对密度的关系莫衷一是。部分学者认为变化遵循如下关系[5]：εd=1-kρ,其中k=1.4～2.0[6],而Lopatnikov等则认为应该取k=1。王鹏飞给出了另外一种形式的拟合公式：εd=r(1-ρ),式中r为拟合参数。因此，我们假定：

εd=C1-C2ρ                                  (3.18)

式中，C1和C2为拟合参数。

结合公式(3.12),(3.13),(3.18)可得闭孔泡沫铝球头压入时的无量纲压入载荷和无量纲压入深度的关系：

é=[k1+k2×（c1-c2ρ）k3]·(h/R)k4+k5（c1-c2ρ）            (3.19)

因此，我们得到压入载荷F与温度T、相对密度ρ和压入深度h的关系为

F=πR2σ0ysCρn（1-T/Tm）·[k1+k2×（c1-c2ρ）k3]·(h/R)k4+k5（c1-c2ρ）           (3.20)

式中，ci(i=1,2)、ki(i=1~5)、C和n都是常数，R是压头半径，Tm是闭孔泡沫铝基体材料的熔化温度，σ0ys为闭孔泡沫铝基体材料在参考温度T=0℃时的屈服强度。对于本文中所用到的闭孔泡沫铝材料：k1=1.80,k2=0.54,k3=-2.15,k4=2.16,k5=-1.18,C=0.3,n=1.5,Tm=660℃。