有限元计算

利用商业有限元软件ABAQUS进行闭孔泡沫铝压入响应的数值模拟。构造轴对称二维模型，模型轴向尺寸100 mm,径向尺寸200 mm,都分别远大于压头半径R=10mm,底部采用固支边界条件，压头与泡沫铝材料之间的接触设为无摩擦。为提高计算结果的精确度和计算效率，网格划分从接触点附近的区域向远离接触点的区域逐渐变疏，最小单元大小为0.25mm×0.20mm。计算中，采用位移控制方式加载，加载速率为2mm/s。

本节主要研究εd和h/R对泡沫材料深压入塑性响应的影响，以得到(3.11)式右端的具体表达式。计算中弹性模量和泊松比分别取为定值100GPa和0。

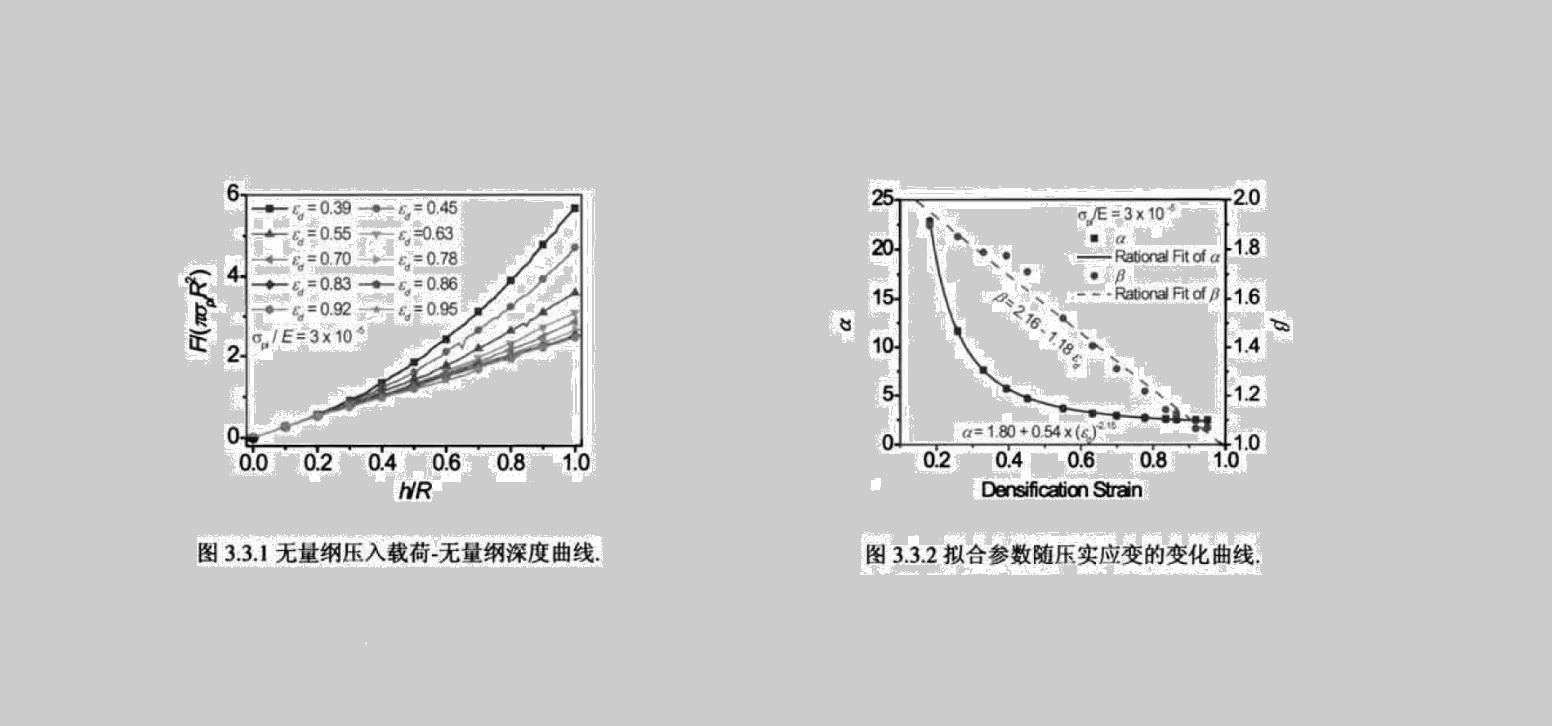
图3.3.1为σpl/E=3×10-5时压实应变εd对无量纲压入载荷F/(πoplR2)与无量纲压入深度h/R关系的影响。由于压入深度h大于压头半径R时，压入变形区域不再增大，变形行为改变，本节只考虑h/R≤1。

从图3.3.1可见，随着压入深度的增大，压入载荷也逐渐增大。随着压实应变的增大，压入相同的深度时，所需压入载荷值降低。这是由于随着压实应变增大，泡沫铝的可压缩性增强，相同载荷值可压入更深的位置。对于图3.3.1,可采用幂函数来拟合不同压实应变下的无量纲参数关系：

é=F/πσplR2=α×(h/R)β                        (3.12)

式中，α和β为待定参数。分别对图3.3.1中的曲线进行拟合后，所得到的拟合参数α和β随压实应变的变化如图3.3.2所示。指数β随着压实应变的增大呈线性递减的关系，即随着压实应变的增大，无量纲压入载荷随着无量纲压入深度增大而增大的速率变缓。

进一步采用如下两个方程来分别拟合α和β随压实应变的关系

α=k1+k2·εdk3              β=k4+k5·εd                             (3.13)

结果得到：k1=1.80,k2=0.54,k3=-2.15,k4=2.16,k5=-1.18。在压入过程中，压头附近已经压实的泡沫材料附着在压头前方随着压头一起向下压入，随着压入深度的增大这部分材料的体积也增大，相当于压头形状变得越来越尖锐。若εd=1,即材料压实后体积为零，压头等效形状不受影响，此时近似有β≈1,即无量纲压入载荷随着无量纲压入深度线性增长。